Le equazioni di struttura stellare
La formazione di una stella consta di tre periodi principali: la formazione della protonube, il collasso della protonube che origina la protostella e la contrazione della protostella verso la fase di sequenza principale. Al raggiungimento di quest’ultima fase, all’interno della stella si avviano le reazioni nucleari che contribuiscono alla fissazione della stella in un fondamentale equilibrio di forze. Possiamo assumere che una stella di sequenza principale sia approssimabile ad un fluido autogravitante, di simmetria sferica, in equilibrio idrostatico e termodinamico, e che il gas stellare sia trattabile come un gas ideale. Saranno necessarie ben sette equazioni per descrivere la condizione di equilibrio di una stella stabile:
- Equilibrio idrostatico;
- Conservazione della massa;
- Conservazione dell’energia;
- Equazioni del trasporto convettivo e radiativo;
- Equazione di stato;
- Opacità della materia stellare;
- Tasso di produzione;
Equazione dell’equilibrio idrostatico
La prima condizione, fondamentale per ritenere la stella un corpo in equilibrio, fissa il bilancio tra la pressione di radiazione e la gravità. Tale equilibrio deve sussistere su ogni strato della stella oppure deve valere, come vedremo, per ogni valore del raggio della stella:
![]()
![]()
Studiamo l’andamento della pressione in un elemento di materia in cui la pressione varia da un raggio r ad uno r+dr, su una superficie infinitesima dS:
![]()
![]()
Sviluppando P(r+dr) come:
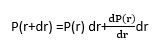
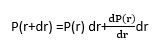
combino le due precedenti equazioni e ottengo il valore della pressione di radiazione:![]()
![]()
Calcoliamo ora il termine di forza di gravità sul medesimo elemento di materia, facilmente reso dalla teoria newtoniana:
![]()
![]()
Riscriviamo l’equazione principale uguagliando i termini delle due forze di gravità e di pressione radiativa, e otteniamo l’equazione finale di equilibrio idrostatico:
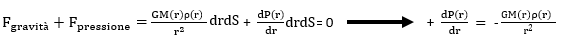
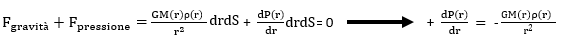
Equazione di conservazione della massa
In regime stazionario, la massa totale entro un certo raggio si conserva, e le variazioni di massa entro tale raggio dipendono strettamente dalla densità. Questo vale per ogni valore di r:


Equazione di conservazione dell’energia
Le stelle presentano al loro interno un gradiente di temperatura che dà origine ad un flusso di energia diretto verso l’esterno. Assumendo che tutta l’energia fluisca mediante diffusione radiativa, l’energia emessa per secondo dalla superficie di una stella di raggio r può essere scritta in funzione della sua luminosità L(r):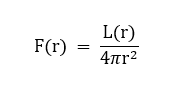
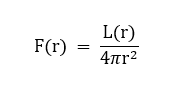
Considerando la densità di materia ρ(r) e il tasso netto di produzione di energia per unità di massa ε(r), in un guscio sferico di spessore dr posto a distanza r dal centro della stella, scriviamo il legame tra il flusso F(r) e la funzione ε(r):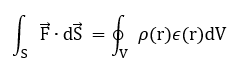
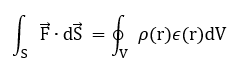
![]()
![]()
Nell’ipotesi di simmetria sferica, scrivendo l’operatore divergenza in coordinate polari, si trova il bilancio di energia per un guscio sferico di raggio r: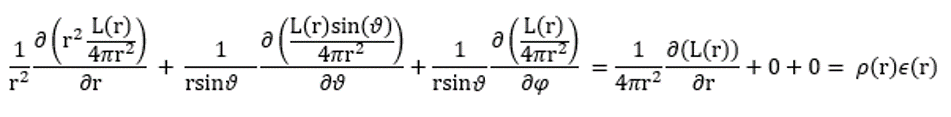
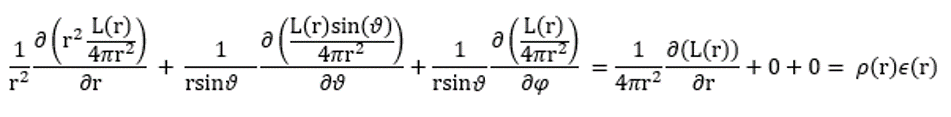
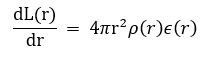
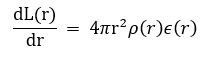
Trasporto radiativo e convettivo dell’energia
L’irraggiamento e la convezione sono i metodi più efficienti di trasporto di energia, prevalenti rispettivamente sulla fotosfera e negli strati interni delle stelle in equilibrio.
- Trasporto radiativo
Ricordiamo il valore di pressione di radiazione, già ricavato dall’equazione di stato:![]()
Tenuto conto della dipendenza della temperatura dal raggio, se deriviamo la formula precedente rispetto a r otteniamo:![]()
![]()
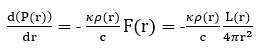
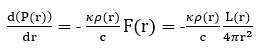
![]()
![]()
- Trasporto convettivo
Il modello più accreditato per spiegare il fenomeno convettivo (Mixing Length) si prefigge di descrivere la convezione come uno spostamento adiabatico di elementi di materia dalla posizione di equilibrio. Alla fine di questo spostamento, stimato di una lunghezza l, segue il rilascio di energia all’ambiente.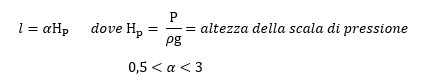
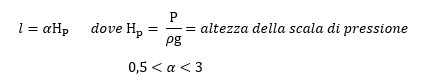
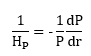
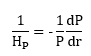
La presenza di instabilità convettive origina i moti convettivi, tale condizione è espressa da:  Se il gradiente di temperatura è prettamente radiativo, il precedente criterio di instabilità convettiva si riscrive:
Se il gradiente di temperatura è prettamente radiativo, il precedente criterio di instabilità convettiva si riscrive: Se, dunque, il gradiente radiativo è maggiore di quello adiabatico, le piccole fluttuazioni nella posizione di un elemento di materia sono in grado di innescare il moto convettivo (instabilità convettiva). Se invece il gradiente radiativo risulta minore di quello adiabatico, per qualsiasi spostamento dell’elemento di materia, questo verrà richiamato alla sua posizione iniziale. Tale condizione è espressa dal criterio di Schwarzschild per la stabilità convettiva:
Se, dunque, il gradiente radiativo è maggiore di quello adiabatico, le piccole fluttuazioni nella posizione di un elemento di materia sono in grado di innescare il moto convettivo (instabilità convettiva). Se invece il gradiente radiativo risulta minore di quello adiabatico, per qualsiasi spostamento dell’elemento di materia, questo verrà richiamato alla sua posizione iniziale. Tale condizione è espressa dal criterio di Schwarzschild per la stabilità convettiva: Assumiamo che tutti gli elementi di materia siano equidimensionati. Quando una bolla di materia avrà percorso la distanza l, questa avrà ceduto una quantità di energia pari a:
Assumiamo che tutti gli elementi di materia siano equidimensionati. Quando una bolla di materia avrà percorso la distanza l, questa avrà ceduto una quantità di energia pari a:
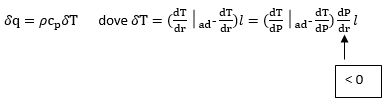
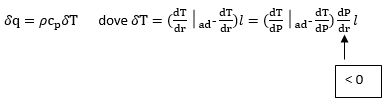
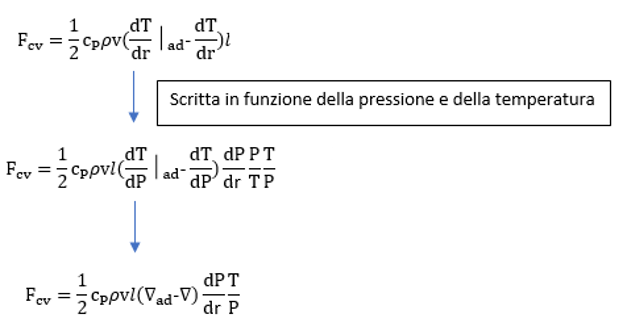

Otteniamo infine la formula del trasporto convettivo: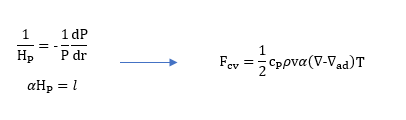

Anche se il trasporto di energia per conduzione è comunque presente, questo risulta essere talmente poco efficiente da essere trascurabile. La conduzione diventa il metodo più efficiente solo in ambienti stellari degeneri, come nelle stelle di neutroni.
L’equazione di stato
Alle temperature tipiche delle superfici stellari – dai 3700 K fino ai 10.000 K – gli atomi si ritrovano completamente ionizzati. Se trascuriamo le interazioni tra le particelle del gas di elettroni e gli ioni, è possibile pensare il gas stellare come un gas ideale, soggetto dunque alla legge di stato dei gas ideali.
Consideriamo la pressione totale come somma di due contributi, dei quali uno dovuto alla radiazione, e l’altro dovuto al gas di elettroni e ioni:
![]()
![]()
Analizziamo prima il contributo del gas di elettroni e ioni. Un gas perfetto, non relativistico e non degenere, può essere trattato con la seguente legge:

Sostituendo il valore di R con il prodotto tra la costante di Boltzmann e il numero di Avogadro, ed esplicitando il termine di pressione, ricaviamo:
![]()
Introduciamo la costante di proporzionalità tra la massa M ed il numero di particelle N, nota come massa molecolare media, che a sua volta si può scrivere come il prodotto tra il peso molecolare medio e la massa della specie chimica mediamente più abbondante, cioè l’idrogeno. Riscriviamo dunque l’equazione di stato come segue:
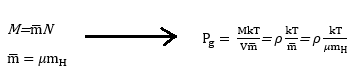

Il peso molecolare medio del gas stellare dipende sia dalla composizione del gas stesso, sia dallo stato di ionizzazione delle singole specie che lo compongono:


Per un gas completamente ionizzato, il peso molecolare medio include sia elettroni sia ioni:
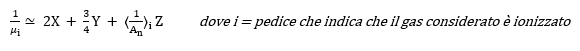
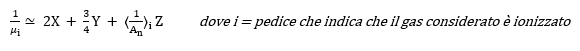
Per le specie più pesanti dell’elio vale che:
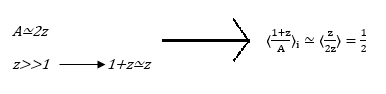
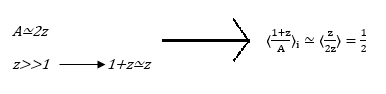
Guardiamo, ora, il contributo di pressione di radiazione. I fotoni possiedono un’energia pari a E=hν, ed un momento pari a P=E/c che viene trasferito nelle fasi di assorbimento o di riflessione. Ciò si traduce in una pressione esercitata dalla radiazione elettromagnetica pari a:
![]()
La pressione totale per un gas perfetto non relativistico di ioni ed elettroni è infine data da:
 Confrontando i due contributi di pressione, si rileva che nelle zone interne del Sole, specialmente al centro, il contributo di pressione di radiazione risulta trascurabile rispetto al contributo di pressione dovuto al gas. La maggiore dipendenza del valore di pressione totale dal gas stellare suggerisce che la convezione sia il metodo di trasmissione dell’energia più efficiente negli interni stellari.
Confrontando i due contributi di pressione, si rileva che nelle zone interne del Sole, specialmente al centro, il contributo di pressione di radiazione risulta trascurabile rispetto al contributo di pressione dovuto al gas. La maggiore dipendenza del valore di pressione totale dal gas stellare suggerisce che la convezione sia il metodo di trasmissione dell’energia più efficiente negli interni stellari.
Opacità della materia stellare
L’opacità influenza fortemente il trasferimento di energia dalle regioni interne della stella allo spazio esterno. In condizioni di equilibrio, la stessa materia stellare mostra un comportamento opaco nei confronti dei fotoni, che vengono continuamente assorbiti o scatterati.
I principali fenomeni di scattering e assorbimento sono:
- Scattering elettrone-fotone: i fotoni vengono diffusi dagli elettroni liberi presenti nel plasma stellare, e come conseguenza il fotone cambia direzione ma non frequenza:
- Assorbimento free-free: si ha l’assorbimento di un fotone da parte di un elettrone libero con la partecipazione di un nucleo nel bilancio energetico;
- Assorbimento bound-free: l’assorbimento di un fotone da parte di un elettrone legato porta l’atomo a ionizzarsi e liberare l’elettrone legato;
- Assorbimento bound-bound: l’assorbimento di un fotone da parte di un elettrone legato comporta l’eccitazione di quest’ultimo da uno stato energetico inferiore ad uno superiore. Questo genere di assorbimento produce righe spettrali nello spettro delle atmosfere stellari.
Ognuno dei fenomeni di assorbimento è accompagnato da fenomeni di emissione stimolata, che aggiungono fotoni al flusso totale. Pertanto, il contributo totale di opacità della materia stellare si compone di cinque elementi:


Tasso di produzione
Il tasso di produzione di energia indica la quantità di energia prodotta da un ciclo di reazioni termonucleari per unità di massa e di tempo, e il suo valore dipende strettamente dalla temperatura dell’ambiente stellare e dalla sezione d’urto. Sul concetto di sezione d’urto, si pensi ad un flusso di particelle diretto verso una particella-bersaglio. L’urto potrebbe non avvenire per tutte le particelle, per cui in ambito nucleare si parlerà di sezione d’urto come la superficie sulla quale è più probabile che avvenga l’impatto tra il flusso di particelle incidenti e la particella-bersaglio.
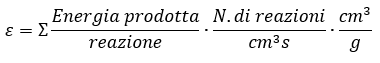
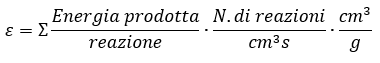
Il parametro ε è funzione della sezione d’urto e della quantità di energia prodotta, entrambe dipendenti dai diversi tipi di reazione nucleare. All’interno delle stelle avvengono tre tipi di reazione di fusione, ovvero il ciclo protone-protone, il ciclo CNO, e il ciclo tripla-α, dei quali riporteremo i singoli tassi di produzione:

Sulla dipendenza dei tassi di produzione di energia dalla temperatura, è fondamentale notare che i primi due cicli avvengono normalmente in stelle che detengono masse e temperature paragonabili a quelle del Sole. Il ciclo tripla-α, invece, domina in ambienti ricchi di elio, tipici di stelle in evoluzione avanzata e con temperature superiori a quelle di stelle di sequenza principale. Vi lasciamo ulteriori approfondimenti sull’energia nucleare e sullo stato tecnologico della fusione sulla Terra.
Fonti
- Ilona Rotaru, Meccanismi di trasporto dell’energia in astrofisica, tesi di laurea, Bologna, 2017/18, Relatore: Prof. Daniele Dallacasa;
- Francesca Dresbach, Principali reazioni termonucleari nelle stelle, tesi di laurea, Bologna, 2017/18, Relatore: Prof. Daniele Dallacasa;
- Davide Di Vita, Le 7 equazioni che regolano la struttura stellare, tesi di laurea, Bologna, 2019/20, Relatore: Prof. Francesco Rosario Ferraro;