Progettiamo una clessidra ad acqua
In questa guida impareremo come ideare una clessidra ad acqua. Tutti conosciamo il funzionamento delle clessidre, quelle classiche dei giochi da tavolo: lo scorrere della “sabbia” contenuta al loro interno indica l’avvenuto passaggio di un certo tempo.
Contrariamente a quanto si possa pensare, non è un’impresa particolarmente complessa quella di progettarne una.
Notazione
Nel seguito verranno utilizzati i seguenti simboli:

Strumenti preliminari
Ciò che ci servirà per poter capire come “progettare” la clessidra sarà la conoscenza di un po’ di calcolo algebrico e differenziale, in aggiunta all’equazione di Bernoulli:
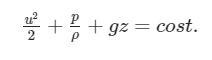
Questa equazione è una delle più note della fluidodinamica e, nonostante valga sotto la verifica di numerose ipotesi, nel nostro caso (il nostro è un caso di flusso incomprimibile soggetto ad un campo di sole forze conservative (come quello gravitazionale) in condizioni di moto stazionario e in assenza di forze viscose; ultima ma non meno importante delle ipotesi è quella che il flusso venga studiato lungo una linea di corrente (direzione parallela alla velocità) per poter trascurare i termini di vorticità, tutte saranno soddisfatte consentendoci di giungere alla soluzione.
Idea di partenza
L’idea di partenza per questo progetto è il classico problema del calcolo del tempo di svuotamento di un serbatoio che, per semplicità di pensiero, immagineremo cilindrico. Supponendo di riempire il serbatoio con acqua (la cui densità è praticamente costante, ρ=1000 (kg)/(m^3) è possibile scrivere l’equazione di Bernoulli tra il cosiddetto (pelo libero) dell’acqua (punto A in figura 1) e il foro di uscita del recipiente, supposto circolare con diametro d (punto B nella stessa figura).

Partendo da quest’esempio, l’equazione ci dice che:
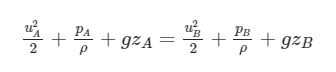
cioè che l’energia totale del sistema tra sezione di ingresso A (il pelo libero) e di uscita B (il foro) si conserva.
A questo punto, siamo abituati a semplificare l’equazione sopra dicendo che la velocità u(A) è molto minore di u(B) e che quindi la possiamo trascurare (vedremo poco più avanti che non è così scontata come semplificazione), che vale l’uguaglianza p(A)=p(B)=p(atm) (supponendo di effettuare il progetto in atmosfera) e che z(B)=0, ponendo così z(A)=h, con h altezza massima del serbatoio rispetto alla quota di riferimento z(B).
Si ottiene dunque
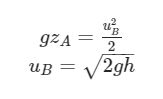
Precisazioni
Se si osserva bene l’equazione precedente, si vede che la condizione per cui la velocità in uscita dal serbatoio è più una condizione iniziale: infatti, l’altezza del pelo libero dell’acqua sarà h soltanto all’inizio dello svuotamento, e tale altezza diminuirà mano a mano che il fenomeno prosegue.
Quindi l’altezza h deve essere intesa come una funzione del tempo, ad esempio esprimibile con z(t). Quello che otteniamo in realtà è
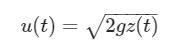
dove abbiamo rimosso il pedice B per semplificare la notazione.
Da questo risultato vediamo che la velocità di svuotamento non è costante (come l’ipotesi iniziale poteva portarci a pensare) ma varia in funzione dell’altezza che, a sua volta, varia in funzione del tempo. Il problema sembra quindi essersi complicato non poco, ma possiamo “fare un po’ di conto” e trovare una comoda soluzione.
Sviluppo e soluzione
Il modo più comodo per procedere è quello di considerare la variazione di volume dell’acqua nel recipiente: dovendo conservarsi la massa si ha che il volume d’acqua che si abbassa deve essere pari al volume di acqua che esce. Considerando elementi infinitesimi si può dunque scrivere:
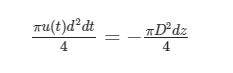
cioè il volume di altezza dx=u(t) dt e base d che esce è pari al volume di base D ed altezza dz che si abbassa. Essendo dt e dz dei differenziali essi sono dotati di segno, ed essendo il dt>0 sicuramente, non può che essere dz<0: da qui il segno meno.
L’equazione ci dà uno spunto di riflessione: se vogliamo sapere quanto tempo ci vorrà per svuotare il recipiente, ci conviene rendere la velocità di svuotamento costante, e di conseguenza l’abbassamento. Facendo le dovute semplificazioni si ottiene:
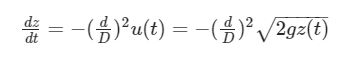
Da quest’ultima equazione vediamo quindi che la velocità di uscita u ed abbassamento dz/dt sono proporzionali a meno di fattori moltiplicativi. Se riusciamo a rendere la derivata di z costante il problema sarà praticamente risolto.
Leggendo bene l’uguaglianza si vede che la velocità u(t) è una funzione della radice di z. Ciò suggerisce di agire sull’unica variabile che ha senso far variare con l’altezza, e cioè il diametro D del recipiente; in particolare, la funzione che descrive il diametro può essere espressa nel seguente modo:
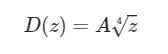
con A una costante da determinare. Il fatto che z sia una radice quarta consente di eseguire la seguente ulteriore semplificazione:
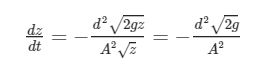
Abbiamo così rimosso la dipendenza dalla variabile z e reso (dz)/(dt) una costante.
L’equazione appena scritta è una differenziale a variabili separabili: portiamo dt a secondo membro e risolviamo gli integrali
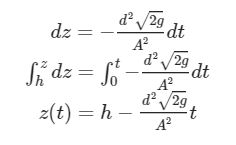
Questa è la funzione esatta di abbassamento del pelo libero dell’acqua che si ha se D è espresso nella forma scritta precedentemente.
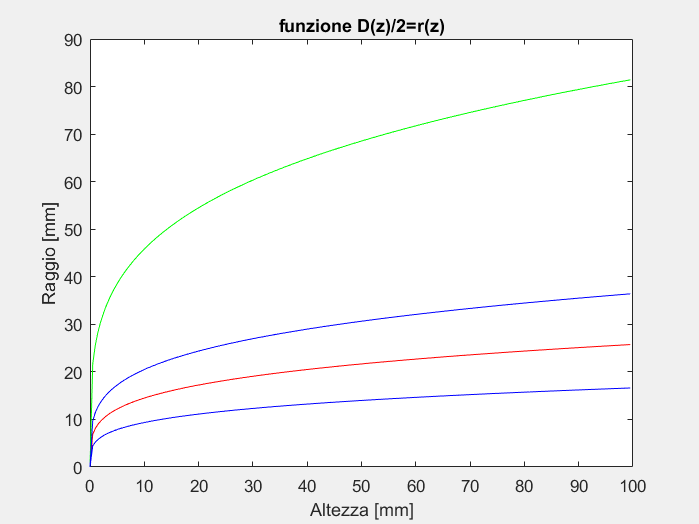
Possibili andamenti di r(z) al variare di T, h, d.
Tenendo conto del fatto che z(T)=0 si determina la costante
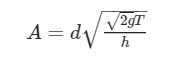
e dunque la forma finale del recipiente, che avrà un diametro
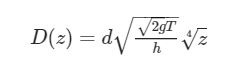
dove con T indichiamo il tempo finale (cioè quello per cui il serbatoio si svuota tutto).
Calcolo dimensionale
Per verificare se la funzione trovata è effettivamente un diametro, quindi espresso in un’unità di lunghezza, possiamo risolvere l'{equazione dimensionale} associata:

Ipotesi velocità trascurabile
Abbiamo visto che u(t) e (dz)/(dt) sono proporzionali a meno del fattore (-d^2)/(D^2). Ciò suggerisce che se D=cost e D>> d (circa 5-10 volte) allora si ha ![]() e l’approssimazione u(A)=0 risulta accettabile.
e l’approssimazione u(A)=0 risulta accettabile.
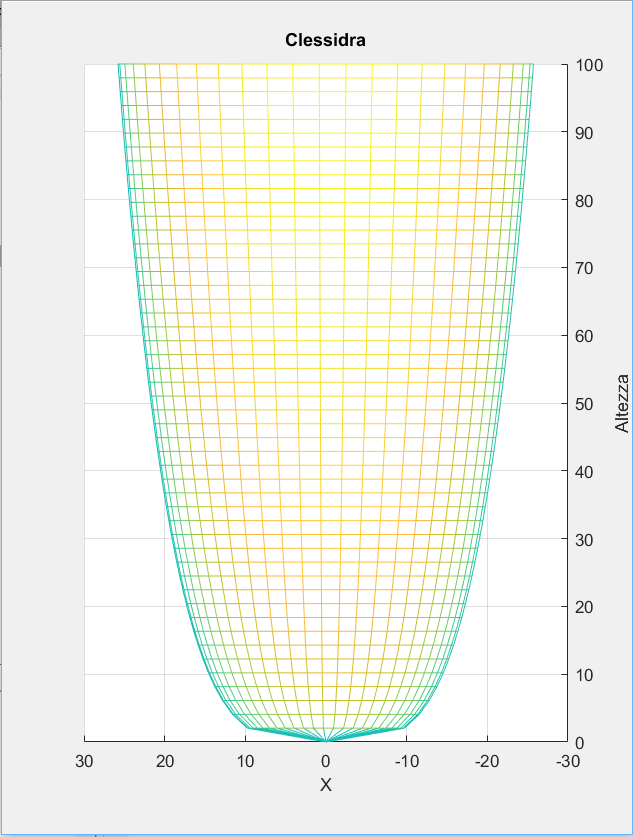
La forma finale di metà clessidra.
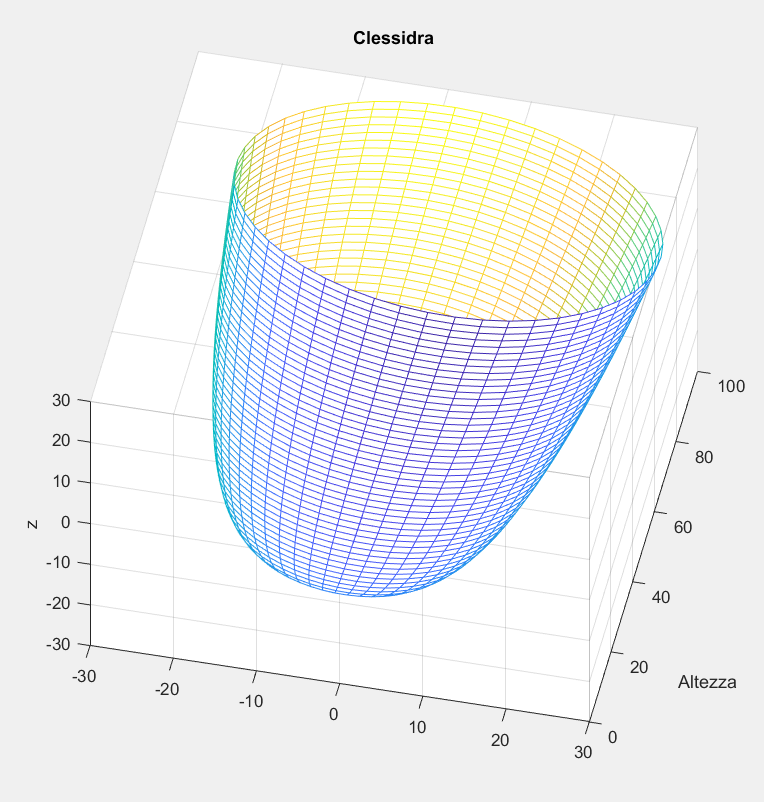
Vista 3D.
Fonti
- Lezioni di Fluidodinamica, R. Verzicco, 2001
- http://www.claredot.net/it/sez_Fluidica/fl04/time_emptying.png
- http://enotecnicalbese.it/files/2013/03/awaglass-bolle-di-sapone-in-una-clessidra.jpg


















très intéressant, je vais essayer à la construire.